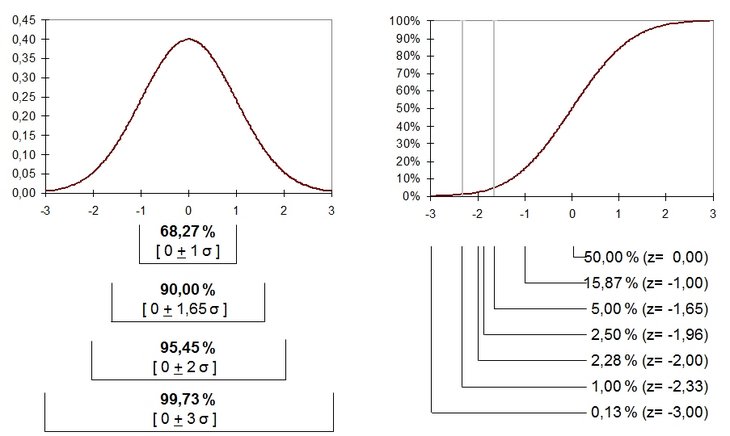
Die Normalverteilung (Gauß-Verteilung) ist eine symmetrische Glockenkurve und bildet den Kern des Varianz-Kovarianz-Modells (vgl. Abbildung oben). Mit den beiden Parametern Erwartungswert und Standardabweichung wird die Verteilung vollständig beschrieben. Für die Risikomessung wird die Standardabweichung mit einem Faktor für die gewünschte Wahrscheinlichkeit der Aussage multipliziert. Die Gültigkeit der Normalverteilungsannahme vorausgesetzt, führt der z-Wert 1,6449 zu einer Aussagewahrscheinlichkeit von 95 Prozent und der z-Wert von 2,3263 zu 99 Prozent. Dabei ist zu beachten, dass die z-Werte ein zweiseitiges Vertrauensintervall beschreiben. Der z-Wert von 1,6449 umschließt ein zweiseitiges Vertrauensintervall um den Mittelwert das 90 Prozent der Wahrscheinlichkeitsmasse beinhaltet. Vereinfacht ausgedrückt liegen links davon 5 Prozent mit Risiken und rechts davon 5 Prozent mit Chancen. Für die Risikoaussage werden die 5 Prozent mit Chancen den 90 Prozent in der Mitte zugeschlagen und ergeben die gewünschten 95 Prozent Aussagewahrscheinlichkeit. 

Der Value at Risk einer einzelnen Vermögensposition ergibt sich aus der Multiplikation von ihrem Marktwert mit seiner Volatilität in Prozent und dem Z-Wert. Bei einer Aktie A mit dem Kurs 100 und einer Volatilität von 20 Prozent p. a. ergibt sich der Value at Risk mit 95-prozentiger Wahrscheinlichkeit auf einen Planungshorizont von einem Jahr wie folgt: 100 * 0,20 * 1,6449 = 32,90. Mit 95 Prozent Wahrscheinlichkeit wird unter normalen Umweltbedingungen binnen eines Jahres der Kursverlust nicht größer als 32,90 sein. 

Setzt sich ein Portfolio aus mehreren unterschiedlichen Vermögenspositionen zusammen, bedarf es einer Aggregation der einzelnen Value-at-Risk-Beträge zu einem Portfolio-Value-at-Risk. Bei einer einfachen Addition der Risikobeträge würden die häufig vorhandenen Diversifikationseffekte unbeachtet bleiben. Eine Aussage über die mögliche Diversifikationswirkung zwischen zwei Vermögenspositionen liefert deren Korrelationskoeffizient. Die risikodiversifizierende Wirkung des Korrelationskoeffizienten wird für ein Beispiel-Portfolio berechnet. Zu der oben beschriebenen Aktie A wird eine zweite Aktie mit dem gleichen Kurswert 100 jedoch einer Volatilität von 30 Prozent p. a. hinzugefügt. Deren Value at Risk beträgt mit 95-prozentiger Wahrscheinlichkeit für einen Planungshorizont von einem Jahr folgerichtig: 100 * 0,30 * 1,6449 = 49,35. 

In einem zweiten Schritt stellt sich die Frage nach der korrekten Aggregation beider VaR-Kennzahlen. Die einfache Addition der beiden Value-at-Risk-Werte führt zu einem Gesamtrisiko von 82,25 bei einem Gesamtvermögen von 200. Bei der Addition zwischen den beiden Risikofaktoren wird implizit eine Korrelation von 1 angenommen. Jedoch sind in der Praxis häufig geringere Korrelationen zwischen Risikofaktoren beobachtbar. Mit einer Korrelation unter 1 können Risikodiversifikationseffekte realisiert werden, die in der bisherigen Berechnung noch nicht betrachtet wurden. Die Korrelation zwischen den beiden Risikofaktoren kann mit Hilfe der nachfolgenden Gleichung berücksichtigt werden, welche an eine Formel aus dem Portfolio-Selection-Modell von Markowitz zur Berechnung des Portfoliorisikos im Zwei-Anlagen-Fall angelehnt ist.

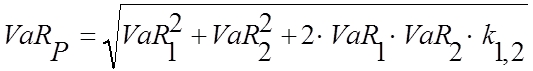
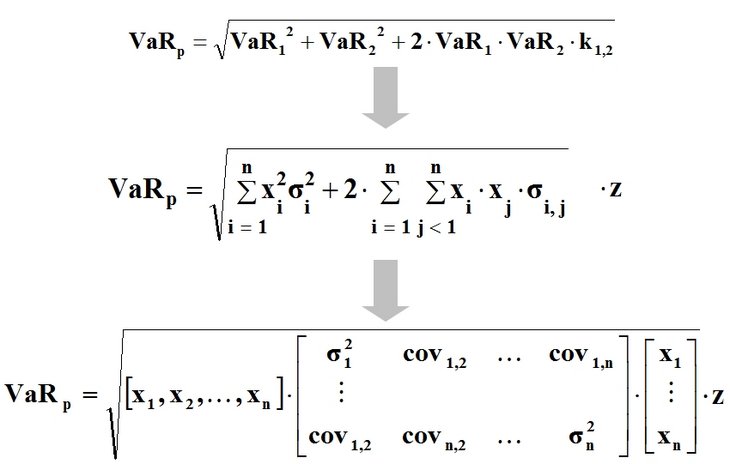
Im Folgenden wird das Gesamtrisiko für den obigen Zwei-Aktien-Fall unter der Annahme einer Korrelation zwischen A und B von Null gerechnet. Der Value at Risk des Portfolios ergibt sich aus

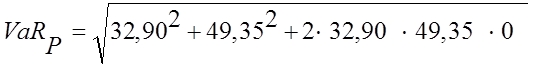
und beträgt 59,31 mit 95-prozentiger Wahrscheinlichkeit auf einen Planungshorizont von einem Jahr. Gegenüber dem undiversifizierten Value at Risk der zu 82,25 addierten Einzelrisiken entspricht dieser Wert einer Reduktion von knapp 30 Prozent. Für den Fall von mehr als zwei Wertpapieren wird statt der oben gezeigten Formel mit einer Wurzel dann eine Matrizenmultiplikation verwendet (vgl. Abbildung unten). In den Matrizen stehen die Varianzen und statt der Korrelationen die Kovarianzen der Risikofaktoren woraus der Name des für beliebig viele Risikofaktoren gültigen Modells resultiert: Varianz-Kovarianz-Modell [vgl. Romeike/Hager 2013, S. 313 ff].

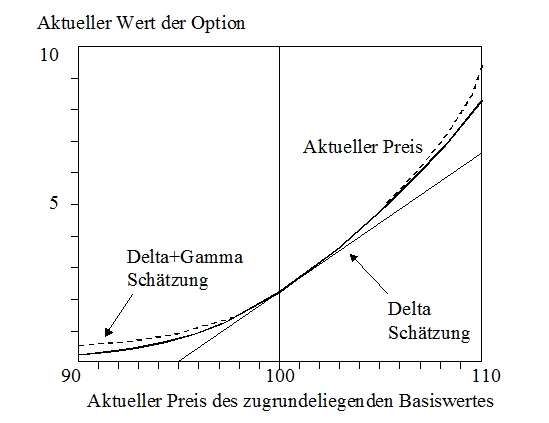
Das Varianz-Kovarianz-Modell existiert in zwei Varianten, dem Delta-Normal-Ansatz und dem Delta-Gamma-Ansatz. Der Delta-Normal-Ansatz unterstellt, dass die Marktwerte der Positionen im Portfolio linear auf Veränderungen der Risikofaktoren reagieren und ist daher für die Risikoberechnung von Portfolios mit symmetrischen Gewinn-/Verlustprofilen geeignet. Die zweite Methode des Varianz-Kovarianz-Modells bildet der Delta-Gamma-Ansatz. Darin wird die Veränderung des Δ durch eine weitere Kennzahl berücksichtigt. Das Г (Gamma) gibt die Veränderungsrate des Δ bezüglich der Veränderung des Kassakurses an. Nachfolgende Abbildung zeigt den konvexen Zusammenhang zwischen der Wertänderung eines Basisinstruments (beispielsweise einer Aktie) und einer darauf bezogenen Option. Das Gewinn-/Verlustprofil von Optionen ist asymmetrisch, gegen Zahlung einer Prämie werden nur die Chancen realisiert und Risiken vermieden. Im Gegensatz zu der Annahme einer linearen Beziehung im Delta-Normal-Ansatz kann die Delta-Gamma-Variante die Konvexität der Wertebeziehung näherungsweise abbilden. So lässt sich approximativ die Wertänderung der Option bei einer kleinen Wertänderung des Basiswertes schätzen. Trotzdem liefert auch der Delta-Gamma-Ansatz nicht die exakten Ergebnisse wie sie bei einer Neubewertung der Position zu erzielen sind.

Die zuerst genannte Delta-Normal-Methode hat gegenüber allen anderen Methoden zur Risikomessung einen Vorteil: Die besonders schnelle und einfache Risikoschätzung. Davon abgesehen benötigt das Modell eine Reihe von Annahmen, die in der Realität nicht vollständig erfüllt sind. Am häufigsten wird die Annahme normalverteilter Veränderungen der Risikofaktoren kritisiert. Die Delta-Normal-Methode führt zu falschen Risikoprognosen, wenn in dem betrachteten Portfolio Optionen enthalten sind. Das Ausmaß des Fehlers wächst mit dem Portfolioanteil asymmetrischer Produkte. Als Alternative wird die Delta-Gamma-Methode zur Lösung des Problems vorgeschlagen. Die Anwendung der Delta-Gamma-Methode liefert für Portfolios mit optionalen Produkten exaktere Value-at-Risk-Schätzungen als die Delta-Normal-Methode. Dennoch kommt es auch bei der Delta-Gamma-Methode zu fehlerhaften Risikoeinschätzungen, wenn die Restlaufzeit der Optionen gegen Null strebt und/oder die Optionen im Geld sind.

Für die Praxis kann das Varianz-Kovarianz-Modell als erste schnelle Lösung dienen, um beispielsweise einen ersten Eindruck von den aktuell bestehenden Risiken zu erhalten. So könnte die tägliche Risikoüberwachung mit einem Varianz-Kovarianz-Modell erfolgen und in gewissen Abständen wären die Risikoschätzungen mit Hilfe von exakteren, aber komplexen und rechenaufwendigen Modellen zu prüfen.