Warum Value at Risk?
Bei Banken und auch Versicherungen hat die Risiko-Kennzahl "Value at Risk" seit Mitte der 90er Jahre einen fast kultartigen Status erreicht. In den letzten Jahren wird sie auch vermehrt in anderen Branchen und Risikobereichen angewendet. Übersetzt man "Value at Risk" wörtlich, so erhält man den "gefährdeten Wert" oder das "Vermögen das einem Risiko ausgesetzt ist". Doch was steckt genau hinter dieser Kennzahl? Inwieweit ist sie geeignet, ein Risiko korrekt zu bewerten?
Die statistischen Bewertungskonzepte des Risikomanagements sind vielfältig: Sie reichen von einfachen Checklisten über die Extremwert-Theorie bis zu neuronalen Netzen. Insbesondere die Finanzdienstleister haben in den vergangenen Jahrzehnten ausgefeilte statistische und mathematische Methoden zur risikoadäquaten Berechnung der Prämien entwickelt.
Viele "Finanzingenieure" unterliegen jedoch dem Trugschluss, man könne die komplexe (Wirtschafts-)Welt mit einer Maschine vergleichen, die nach klaren Ursache-Wirkungsketten funktioniert und daher mit bestimmten interdependenten Verhaltensgleichungen auch modelliert werden kann. Trotz aller Fehlprognosen überwiegt der Charme einer Risikoaussage mit einem konkreten Zeithorizont, Risikobetrag und einer Wahrscheinlichkeit. Vor diesem Hintergrund hat sich in den vergangenen Jahren der Value at Risk als "Standard-Risikomaß" herausgebildet.
Die Geburtsstunde des Value at Risk
Dennis Weatherstone verlangte während seiner Zeit als Vorsitzender der US-amerikanischen Investmentbank J.P. Morgan täglich um 16.15 Uhr einen einseitigen Risiko-Bericht, in dem das gesamte Marktexposure des Handelsbestandes der Bank sowie eine Schätzung der möglichen Verluste in den folgenden 24 Stunden dargestellt waren. Weatherstone war es einfach leid, dass die Marktrisiken der verschiedenen Finanzinstrumente mit unterschiedlichen Methoden gemessen wurden. Sein bisheriger Report enthielt eine Unmenge von Beta-Faktoren und Volatilitäten, gearing factors, Deltas, Gammas und Thetas. Er wollte ein einheitliches Risiko-Maß für alle Finanzinstrumente haben.
Dies war die Geburtsstunde des "Report 4.15". Im Oktober 1994 veröffentlicht J.P. Morgan sein Produkt RiskMetrics™ und stellten es allen Interessenten unentgeltlich zur Verfügung (www.jpmorgan.com/). Im Kern basiert dieses Produkt auf einer Methodik, die als "Value at Risk" bezeichnet wurde.
Definition und Berechnung des Value at Risk
Definiert wird der Value at Risk als der absolute Wertverlust einer im Unternehmen definierten Risiko-Position, der mit einer zuvor definierten Wahrscheinlichkeit (Konfidenzniveau) innerhalb eines fest bestimmten Zeitraums (Halteperiode) nicht überschritten wird [von Balduin 2003, S. 41 sowie Romeike/Hager 2009, S. 203 und Romeike/Hager 2013, S. 191].
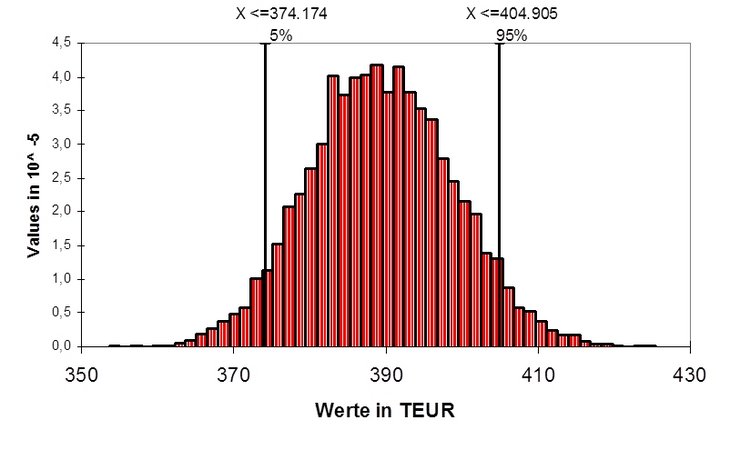
In der folgenden Abbildung wird der Value at Risk dargestellt. Von den simulierten Vermögenswerten liegen 90 Prozent in dem Intervall zwischen 374.174 und 404.905 EUR. Je 5 Prozent liegen drüber oder drunter. In der Regel wird ein noch höherer Vermögenswert nicht als Risiko ("downside risk") angesehen, so dass die 5 Prozent extrem guten in die Wahrscheinlichkeit eingerechnet werden, mit der eine Verlustmarke nicht unterschritten werden kann. In dem konkreten Beispiel lautet die Aussage: Mit 95 Prozent Wahrscheinlichkeit wird das Vermögen nicht unter den 374 TEUR liegen.
Für die Berechnung des Value at Risk müssen bestimmte Voraussetzungen erfüllt sein:
- Die Risiken müssen in Einzelkategorien zerlegt und mit einer geeigneten Verteilungsfunktion beschrieben werden,
- die Abhängigkeiten zwischen den Risiken sollten bekannt sein bzw. geschätzt werden können,
- die Eigenschaften der Risiken müssen im Zeitablauf einigermaßen stabil und prognostizierbar sein (Extremszenarien werden nicht berücksichtigt),
- es muss eine gesicherte Datenbasis vorhanden sein.
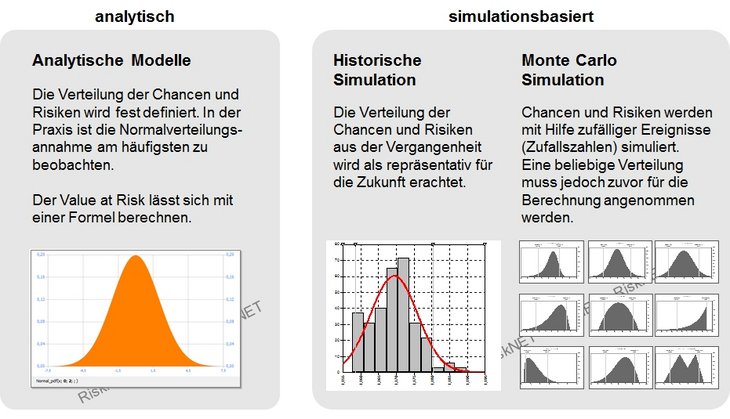
Zur Messung des Value at Risk kann man grundsätzlich zwischen zwei verschiedenen Ansätzen unterscheiden: Einem analytischen Ansatz und einem Simulationsansatz [vgl. Eisele/Knobloch 2000, 160f.].
Diese beiden Ansätze unterscheiden sich im Wesentlichen in zwei Punkten, nämlich der Modellierung der Entwicklung der Risikofaktoren und der Sensibilität der betrachteten Portfolios bzw. Positionen. Während im Rahmen des analytischen Ansatzes das Modell auf der Grundlage von bekannten Zusammenhängen und Beziehungen zwischen den einzelnen Variablen mit Hilfe einer Verteilungsannahme gebildet wird, errechnet sich der Value at Risk beim Simulationsansatz anhand der Simulation verschiedener Zustandsentwicklungen.
Die Historische Simulation bedient sich dabei vergangenheitsbezogener Daten. Hierbei wird unterstellt, dass alle Risikofaktoren aus der Vergangenheit auch in Zukunft den Wert der Risikoposition in gleicher Weise beeinflussen werden. Die Historische Simulation ist wegen ihres geringen mathematischen Anspruchs einfach zu implementieren. Die Anwender müssen sich nicht mit der Messung von Volatilitäten und Korrelationen auseinandersetzen. Es werden auch keine Kenntnisse von Loga¬rithmus, e-Funktion, Matrizenmultiplikation oder gar der Simulation von Zufallszahlen benötigt. Der Einfachheit des Ansatzes steht die Beschränkung auf die Vergangenheit gegenüber, was von Kritikern häufig mit dem Lenken eines Autos durch den Blick in den Rückspiegel verglichen wird. Ist der gewählte historische Zeitraum nicht repräsentativ für die Zukunft, schlägt das Modell fehl. Ebenso können keine Ereignisse simuliert werden, die zwar möglich aber noch nie beobachtet worden sind.
Die stochastische Simulation (siehe Monte-Carlo-Methode bzw. Monte-Carlo-Simulation) basiert nicht auf historischen Werten, sondern auf einer stochastischen Variation der unterschiedlichen Modellparameter. Im Rahmen dieses stochastischen Ansatzes werden neben den einzelnen Risiko-Positionen und ihren Einflussfaktoren auch die Korrelationen zu anderen Risiko-Positionen berücksichtigt.
Die stochastische Simulation gilt wegen ihrer Flexibilität gegenüber anderen Verfahren als überlegen, insbesondere bei der Risikomessung von komplexen Exposures wie sie beispielsweise aus Derivaten resultieren. Die Monte Carlo Simulation kann beliebige Verteilungen, Restlaufzeitverkürzungseffekte, Volatilitätsclustering, fat tails, nichtlineare Exposures und Extremszenarios in der Risikoberechnung berücksichtigen. Als Nachteile sind der hohe Rechenaufwand und die Komplexität der eingesetzten statistischen Verfahren zu nennen.
Dem gegenüber hat das analytische Verfahren eine je nach Anwendungsfall ähnliche Komplexität, erzeugt jedoch deutlich weniger Rechenaufwand. Der sogenannte Varianz-Kovarianz-Ansatz weist aber den häufig kritisierten Nachteil auf, dass für alle Risikofaktoren eine Normalverteilung unterstellt wird. Für die Praxis kann das Varianz-Kovarianz-Modell als erste schnelle Lösung dienen, um beispielsweise einen groben Eindruck von den aktuell bestehenden Risiken zu erhalten.
Grenzen des Value at Risk
Wie jede Modellbildung stellt auch die Berechnung des Value at Risk eine Gradwanderung zwischen Komplexität und Genauigkeit dar. So bauen etwa die analytischen Bewertungskonzepte auf normalverteilten Einzelrisiken auf, da die entstehenden Modelle ansonsten zu komplex und dadurch nicht mehr handhabbar wären. Ähnliche Kompromisse müssen auch bei den Verfahren der Historischen und der Monte Carlo Simulation eingegangen werden. Hier wird zwar in der Regel auf die Annahme der Normalverteilung verzichtet, allerdings kann naturgemäß nur eine endliche Auswahl der unendlichen Anzahl möglicher Entwicklungen und Umweltgegebenheiten berücksichtigt werden. Einerseits stellen diese Vereinfachungen und Einschränkungen eine notwendige Voraussetzung dar, um die Berechnung überhaupt durchführen zu können. Andererseits führen sie aber auch zu Ungenauigkeiten, da das Modell immer unvollständig bleiben muss.
Neben diesen methodischen Defiziten, die zwangsläufig in Kauf zu nehmen sind, wird auch die ökonomische Interpretation der Kennzahl Value at Risk häufig kritisiert. Als Ergebnis der Berechnungen wird ein Wert angegeben, der mit einer festgelegten Wahrscheinlichkeit von beispielsweise 95 Prozent nicht überschritten wird. Bei einer solchen Definition werden jedoch die Risiko-Werte mit einer Wahrscheinlichkeit von größer 95 bis 100 Prozent nicht berücksichtigt. Würde man das Konfidenzniveau auf 99,5 Prozent erhöhen, könnte eine größere Anzahl an Szenarien abgebildet werden, eine unbekannte Restgröße mit einer sehr geringen Eintrittswahrscheinlichkeit würde jedoch auch hier erhalten bleiben (0,5 Prozent). Allgemein formuliert kann das β-Perzentil auch als 200-Jahresereignis interpretiert werden. Bei einem 200-Jahresereignis geht es um ein Schadenereignis, welches im Mittel alle 200 Jahre auftreten wird.
Dabei wird keinerlei Aussage über die Periodizität getroffen, das heißt das Schadensereignis muss nicht in Zeitintervallen von 200 Jahren auftreten. Es kann auch beispielsweise fünf Mal hintereinander eintreten, danach lange Zeit nicht mehr und die Modellannahme war trotzdem richtig. Ebenso ist die Wahrscheinlichkeitsaussage mit einer eigenen Irrtumswahrscheinlichkeit belegt, so dass in einem Modellbacktesting von der Wahrscheinlichkeit in berechneten Bandbreiten nach unten und oben abweichende Beobachtungen zulässig sind ohne dass das Modell abgelehnt werden könnte.
Risikomaß für Sonnenwetter und Schlechtwetter
Etwas überspitzt kann gesagt werden, dass der Value at Risk damit genau den Bereich der Wahrscheinlichkeitsverteilung nicht betrachtet, die für das Überleben eines Unternehmens (und damit für das Risikomanagement) besonders relevant ist. Damit kann der Value at Risk auch als Schönwetter-Risikomaß interpretiert werden.
Während für Weatherstone der Ein-Prozent-Wahrscheinlichkeitsbereich akzeptabel war, sollte man vorsichtig sein, dies auch auf Kreditrisiken, Derivate oder operationelle Risiken zu übertragen. Gerade die Ereignisse des 11. September 2001, die Flutkatastrophe vom August 2002 in Mittel- und Osteuropa oder das Tōhoku-Erdbeben im Jahr 2011haben gezeigt, dass gerade diese "low frequency, high severity"-Ereignisse (Extremereignisse) fatale Auswirkungen haben können.
Ergänzende Methoden wie die Szenarioanalyse oder die Extremwerttheorie (Extreme Value Theory) können helfen, diese Informationslücke bei der Risikoquantifizierung zu minimieren. Außerdem bietet der Werkzeugkasten des Risikomanagements alternative Risikomaße, wie beispielsweise den Expected Shortfall (ES). Der ES wird auch als "conditional value at risk" (CVaR), "average value at risk" (AVaR) oder "expected tail loss" (ETL) bezeichnet. Des ES zählt wie der VaR zu den Downside-Risikomaßen und ist definiert als der erwartete Verlust für den Fall, dass der VaR tatsächlich überschritten wird. Somit ist er der wahrscheinlichkeitsgewichtete Durchschnitt aller Verluste, die den VaR-Wert übertreffen. Es werden daher nur die Verluste betrachtet, die über den VaR hinausgehen.
Unter den Lower Partial Moments (LPM) werden Risikomaße verstanden, die sich als Downside-Risikomaß nur auf einen Teil der gesamten Wahrscheinlichkeitsdichte beziehen. Sie erfassen nur die negativen Abweichungen von einer Schranke bzw. Zielgröße, werten hier aber die gesamten Informationen der Wahrscheinlichkeitsverteilung aus (bis zum theoretisch möglichen Maximalschaden.
Das Phänomen Risiko weist zahlreiche Facetten auf, denen man nur mit einem Portfolio an Methoden zur Identifikation und Quantifizierung gerecht werden kann. Risikomanagement kann nie die Suche nach einem einzigen, "optimalen" methodischen Ansatz sein. Ein Risiko-Messsystem, dass uns "blind" gegenüber anderen, vom Modell nicht erfassten Risiken macht, suggeriert uns eine falsche Sicherheit vor und ist daher auch als Risiko-Überwachungssystem fragwürdig.
Weiterführende Literaturhinweise:
- Balduin, A. von (2003): Operational Value at Risk – Ein Ansatz für das Management von Operationellen Risiken, RiskNews 01/2003.
- Bankhofer, U. et al (1999): Mathematische Methoden in der Versicherungswirtschaft – eine empirische Studie, Arbeitspapiere zur Mathematischen Wirtschaftsordnung, Augsburg 1999.
- Eisele, W./Knobloch, A. P. (2000): Value at Risk: Tool for Managing Trading Risk, in: Frenkel, M.; Hommel, U.; Rudolf, M.: Riskmanagement – Challenge and Opportunity, Heidelberg 2000, S. 155-179.
- Hager, P. (2004): Corporate Risk Management – Value at Risk und Cash Flow at Risk, Frankfurt/Main 2004.
- Leippold, M. (1998): Value at Risk – Standard mit Schönheitsfehler, Schweizer Bank 08/1998.
- Romeike, F. (2009): Was ist der "Value at Risk"? Oder besser: Was ist er nicht?, in: Risk, Compliance & Audit (RC&A), 03/2009, S. 10-11.
- Romeike, F./Hager, P. (2009): Erfolgsfaktor Risk Management 2.0 – Methoden, Beispiele, Checklisten: Praxishandbuch für Industrie und Handel, 2. Auflage, Wiesbaden 2009.
- Romeike, F./Hager, P. (2013): Erfolgsfaktor Risk Management 3.0 – Methoden, Beispiele, Checklisten: Praxishandbuch für Industrie und Handel, 3. Auflage, Wiesbaden 2013.