Monte-Carlo-Simulation
Dem Namen nach eine der bekanntesten Simulationsmethoden dürfte die Monte-Carlo-Simulation sein (auch als stochastische Szenarioanalyse bezeichnet; im Gegensatz zur deterministischen Szenarioanalyse). Das liegt sicherlich zu einem nicht unerheblichen Teil am Namen Monte Carlo, der in aller Welt durch das dort befindliche Casino häufig mit Glücksspiel assoziiert wird. Eng damit verbunden ist der Begriff der Wahrscheinlichkeit, und in der Tat liefern die mathematische Wahrscheinlichkeitstheorie und die Statistik das wissenschaftliche Fundament dieser Simulationsmethode.
Die Entwicklung der Methode ist eng verbunden mit den Namen der beiden Mathematiker Stanislaw Ulam und John von Neumann. Sie sollen während ihrer Arbeit zum Manhatten-Projekt am Los Alamos Scientific Laboratory diese Methode verwendet haben, um hochkomplexe physikalische Probleme nummerisch mit Hilfe einer Simulation zu lösen [vgl. Hubbard 2007, S. 46 sowie Grinstead/Snell 1997, S. 10-11]. Der Anekdote nach wurde als Codename Monte Carlo verwendet. Die ersten wissenschaftlichen Publikationen zu diesem Verfahren erschienen Ende der 1940er Jahre [vgl. Ulam/Richtmyer/von Neumann 1947]. Mit dem zur damaligen Zeit parallelen Aufkommen elektronischer Computer fand die Monte-Carlo-Simulation zunächst in der Wissenschaft, später auch in der Wirtschaft ihre Verbreitung.
Eine der ersten Monte-Carlo-Simulationen der Geschichte hat jedoch bereits der französische Naturforscher Georges Louis Leclerc de Buffon im 18. Jahrhundert durchgeführt [vgl. Kaiser/Nöbauer 1998, S. 185 und S. 286]. In seinem unterdessen berühmten Nadelexperiment untersuchte er, mit welcher Wahrscheinlichkeit eine zufällig geworfene Nadel die Linien eines parallelen Rasters kreuzt. Diese Wahrscheinlichkeit lässt sich analytisch ermitteln, sie ist unter anderem abhängig von der mathematischen Naturkonstante π. Dieses Verfahren kann jedoch auch umgekehrt benutzt werden, um eben dieses π zu ermitteln. Durch den Zufallscharakter jedes einzelnen Nadelwurfs beruht dieses Verfahren auf dem Prinzip der Monte-Carlo-Methode.
Die grundlegende Idee der Monte-Carlo-Methode ist es, für zufällig gewählte Parameter über die entsprechenden Zusammenhänge (Ursache-Wirkungsgeflecht) die zugehörigen Ergebnis- oder Zielgrößen zu ermitteln. Das zur Ermittlung der Zielgrößen verwendete Modell ist in der Regel deterministischer Natur, das heißt, mit dem Festlegen der Parameter sind die Zielgrößen eindeutig bestimmt. Allerdings sind die Zielgrößen durch den Zufallscharakter der Parameter im Prinzip wiederum zufällige Größen. Jedoch kann im Allgemeinen davon ausgegangen werden, dass eine hinreichend große Anzahl so ermittelter Zielgrößen einen guten Näherungswert für die tatsächlichen Werte dieser Zielgrößen darstellt (genau genommen sind nicht die tatsächlichen Werte, sondern die Erwartungswerte der Zielgrößen gemeint. Mathematisches Fundament dieses Vorgehens sind das Gesetz der großen Zahlen, der Hauptsatz der Statistik, siehe Satz von Gliwenko, sowie der zentrale Grenzwertsatz). Die Monte-Carlo-Methode ist damit ein Stichprobenverfahren. Auf Grund der zufälligen Auswahl der Parameter hat sich ebenfalls der Begriff der stochastischen Simulation etabliert [vgl. vertiefend Romeike/Hager 2013, S. 339 ff. sowie Romeike/Spitzer 2013, S. 101 ff.].
Das Vorgehen bei einer Monte-Carlo-Simulation wurde von Metropolis und Ulam in einem Artikel beschrieben, der im Jahre 1949 im Journal of the American Statistical Association erschienen ist. Darin beschreiben beide Wissenschaftler das Vorgehen bei der Monte-Carlo-Methode durch zwei Schritte: "(1) production of 'random' values with their frequency distribution equal to those which govern the change of each parameter, (2) calculation of the values of those parameters which are deterministic, i.e., obtained algebraically from the others." [Metropolis/Ulam 1949, S. 335-341].
Diese aus heutiger Sicht simple Idee, die Eingangsparameter einer Simulation als Zufallsgrößen zu betrachten, kann auch mit anderen Simulationsansätzen kombiniert werden. So sind stochastische Szenarioanalysen keine Seltenheit, aber auch für nahezu alle weiter unten erläuterten Simulationsmethoden ist die Verwendung stochastischer Parameter heutzutage eine gängige Praxis.
Illustration der Methode
An dem durch Metropolis und Ulam beschriebenen Vorgehen hat sich in den letzten etwa 60 Jahren nicht viel geändert. Illustriert werden soll das Vorgehen an folgendem Beispiel [vgl. Romeike/Spitzer 2013, S. 103 f.]: Ein Servicetechniker betreut zwei Kunden. Kunde A benötigt mit einer Wahrscheinlichkeit von 20 Prozent die Unterstützung des Technikers, während Kunde B lediglich mit einer Wahrscheinlichkeit von 5 Prozent auf Hilfe angewiesen ist. Gesucht ist die Wahrscheinlichkeit, dass beide Kunden, die stochastisch unabhängig voneinander agieren, gleichzeitig den Servicetechniker um Hilfe bitten (die Lösung ist in diesem einfachen Fall auch analytisch ermittelbar, die Wahrscheinlichkeit eines gleichzeitigen Hilferufs beträgt 20 % * 5 % = 1 %).
Soll dieses Beispiel mit Hilfe der Monte-Carlo-Simulation gelöst werden, so wird zunächst eine zufällige Situation erzeugt und für diese geprüft, ob beide Kunden den Techniker um Hilfe bitten. Dies geschieht dadurch, dass zunächst Zufallszahlen für A und B ermittelt werden und jeweils gemäß der angegebenen Wahrscheinlichkeit ein Servicebedarf festgestellt wird. Da gängige Zufallszahlengeneratoren Zufallszahlen zwischen 0 und 1 generieren, kann die Zuordnung Servicebedarf erfolgen, wenn die Zufallszahl des Kunden A kleiner als 0,2 und die des Kunden B kleiner als 0,05 ist. Damit ist der erste Schritt im Vorgehen von Metropolis und Ulam bereits erledigt. Anschließend ist die Zielgröße der Simulation zu ermitteln, was im vorliegenden Fall bedeutet, dass beide Kunden gleichzeitig einen Servicebedarf (beziehungsweise keinen gleichzeitigen Servicebedarf) anmelden. Dies entspricht bereits dem zweiten Schritt des von Metropolis und Ulam beschriebenen Vorgehens.
Diese Abfolge der Schritte 1 und 2 wird nun so lange wiederholt, bis die sich ergebende Verteilung der Zielgröße eine stabile Verteilung zeigt. Wie aus nachfolgender Abbildung ersichtlich, konvergiert die Zielgröße mit steigender Anzahl an Simulationsläufen gegen den bereits analytisch ermittelten Wert von 1 Prozent.
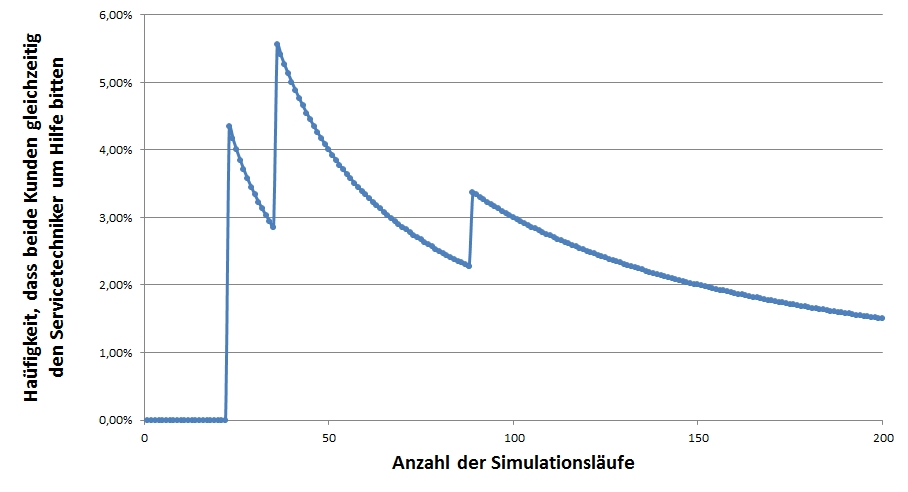
Typische Anwendungsfälle
Generell lassen sich zwei Problemgruppen unterscheiden, bei denen die Monte-Carlo-Methode angewendet werden kann. Mit ihrer Hilfe können einerseits Problemstellungen deterministischer Natur, die eine eindeutige Lösung besitzen, bearbeitet werden. Auf der anderen Seite sind aber auch Fragen, die sich der Gruppe stochastischer Problemstellungen zuordnen lassen, für eine Monte-Carlo-Simulation ein geeignetes Anwendungsfeld. Zum letzten gehört beispielsweise das im vorherigen Absatz beschriebene Beispiel.
Ein typisches und weit bekanntes Anwendungsbeispiel der ersten Problemgruppe ist die Berechnung von Integralen, beispielsweise zur Ermittlung der Zahl π, die hier zum Verständnis der Methode kurz dargestellt werden soll. Bei der auch "Hit or Miss" benannten Methode werden eine große Anzahl zufälliger Wertepaare (x, y) ermittelt, wobei x und y jeweils gleichverteilte Zufallszahlen zwischen 0 und 1 sind. Anschließend wird gezählt, wie viele dieser Wertepaare innerhalb des durch x2+y2 < 1 beschriebenen Viertelkreises befinden. Diese Anzahl der "Treffer" (Hit) bezogen auf die Anzahl aller zufälligen Wertepaare (x, y) ist ein Näherungswert für π/4. Kennzeichnend für dieses Vorgehen ist es, dass das Ergebnis faktisch aus einer zufälligen Stichprobe an Wertepaaren ermittelt wird, obwohl eine analytisch exakte Ermittlung ebenfalls möglich wäre.
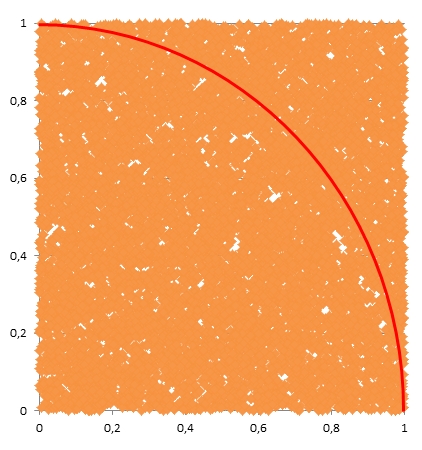
Der mit dem Einsatz der Monte-Carlo-Methode erzielte Vorteil liegt in einer sehr schnellen und einfachen Ermittlung des Ergebnisses. Dafür werden dann durch das Näherungsverfahren entstehende Genauigkeitsverluste im Vergleich zu einer exakten Ergebnisermittlung, die häufig wesentlich aufwändiger und deutlich zeitintensiver ist, bewusst in Kauf genommen. Und so findet die Monte-Carlo-Methode in diesem Problemfeld neben der Berechnung von bestimmten Integralen beispielsweise ebenfalls Anwendung bei der Lösung gewöhnliche und partielle Differentialgleichungen, insbesondere in der Teilchenphysik.
Die zweite Problemgruppe stochastischer Fragestellungen ist dadurch gekennzeichnet, dass die Eingangsparameter und daraus resultierend auch die Zielgrößen stochastischer Natur sind. Damit ist gemeint, dass statt eines wohldefinierten Wertes für den Parameter im einfachsten Fall mehrere mögliche diskrete Werte, jeweils versehen mit einer Eintrittswahrscheinlichkeit, gegeben sind. Im Allgemeinen stammen die Parameter sogar aus einem Kontinuum an Werten, für das eine Wahrscheinlichkeitsdichte, eine sogenannte Verteilungsfunktion, bekannt ist oder gar nur geschätzt wird. Die mit diesen Parametern in Verbindung stehenden Zielgrößen sind dann ebenfalls stochastischer Natur, was heißt, dass sie mittels einer Verteilungsfunktion beschreibbar sind.
Bei geringer Komplexität der Zusammenhänge zwischen Parametern und Zielgrößen und gleichzeitig einfachen Verteilungsfunktionen der Parameter können die Verteilungsfunktionen der Zielgrößen meist noch analytisch ermittelt werden. Schnell ist jedoch eine Grenze erreicht, wo die analytische Ermittlung zu aufwändig wird oder auch gar nicht mehr möglich ist. Hier kommt dann die Monte-Carlo-Methode zum Einsatz. Wie bereits oben beschrieben werden dazu auf Basis der Verteilungsfunktionen zufällige Parameter ausgewählt und für diese werden die zugehörigen Zielgrößen ermittelt. Durch ein vielfaches Wiederholen dieser Ermittlung der Zielgrößen wird für diese eine Häufigkeitsverteilung bestimmt, die eine Näherung für die tatsächliche Verteilungsfunktion der Zielgrößen darstellt.
Aus einer betriebswirtschaftlichen Sicht können somit alle Fragen untersucht werden, die
- entweder aufgrund der Vielzahl ihrer Einflussgrößen nicht mehr exakt analysiert werden (können) und bei denen daher auf eine Stichprobe für die Analyse zurückgegriffen wird;
- oder bei denen die Eingangsparameter Zufallsgrößen sind. (Auch die Optimierung von Prozessen oder Entscheidungen bei nicht exakt bekannten Parametern gehören zu dieser Gruppe.)
Diese beiden Kriterien treffen nun auf eine Vielzahl betriebswirtschaftlicher Entscheidungen zu, dementsprechend finden sich eine ganze Reihe konkreter Anwendungsfälle von Monte-Carlo-Simulationen in betriebswirtschaftlichen Fragestellungen:
- Die Stabilitätsanalyse von Algorithmen und Systemen. Hier werden Monte-Carlo-Simulationen genutzt, um beispielsweise in der Kostenrechnung die Auswirkungen veränderter Aufteiler in der Kostenträgerrechnung auf die Produktkosten zu ermitteln.
- Die Aggregation von Einzelrisiken eines Unternehmens zu einem unternehmerischen Gesamtrisiko. Hierbei wird für jedes Einzelrisiko eine Wahrscheinlichkeitsverteilung geschätzt, um daraus mit Hilfe der Monte-Carlo-Simulation ein aggregiertes Risiko zu ermitteln. Die entstehende Verteilungsfunktion wird in aller Regel auf einzelne kommunizierbare Kennzahlen, etwa Erwartungswert oder ausgewählte Quantilswerte – wie etwa dem Value at Risk oder das Risikokapital – verdichtet.
- Ein wichtiger Schritt zu einer risikoorientierten Weiterentwicklung des Controllings stellt die so genannte "Szenario-Planung" dar. Hierbei werden zukünftige EBIT-Entwicklungen unter Berücksichtigung von Risiken (EBIT-at-Risk) simuliert. Hierbei liegt die Erkenntnis zu Grunde, dass Szenarien und Simulationen bewährte Instrumente aus der Praxis darstellen, um sich mit zukünftigen potenziellen Entwicklungen zu beschäftigen. Eine risikoorientierte Planung verfolgt das Ziel, die traditionelle "einwertige" Planung mit einem Erwartungs- oder Zielwert durch eine realistischere Planung unter Nutzung von Verteilungsfunktionen ("stochastische Planung") zu ersetzen, die sowohl das erwartete Ergebnis als auch den Umfang möglicher Abweichungen (Risiken) beschreiben kann [vgl. vertiefend Romeike 2010, S. 13-19 sowie Romeike/Hager 2014].
- Die Vorhersage von Entwicklungen, die selbst durch zufällige Ereignisse beeinflusst werden (sogenannte stochastische Prozesse). Klassische Beispiele sind die Simulation von Börsen- oder Währungskurse, die auf die Dissertation des französischen Mathematikers Louis Bachelier zurück geht. Basierend auf eigenen Annahmen, gegebenenfalls begründet mit Beobachtungen aus der Vergangenheit, werden hierbei derartige Entwicklungen simuliert und ihre Auswirkungen auf betriebswirtschaftliche Größen analysiert.
- Die Optimierung von eigenen Entscheidungen, die auf unsicheren Annahmen beruhen. Hierunter fallen beispielweise die Gewinnmaximierung bei unsicherem Absatz im Newsvendor-Modell. Im Newsvendor-Modell kauft ein Zeitungsjunge morgens eine Anzahl an Zeitungen, um sie anschließend an seine Kunden weiter zu verkaufen. Nicht verkaufte Zeitungen kann er nur mit Verlust zurückgeben, so dass sich für ihn die Frage seiner optimalen Einkaufsmenge stellt. Ist die Marktnachfrage eine stochastische Größe, so ist die Maximierung seines Gewinnerwartungswerts ist zwar formal-analytisch möglich. Jedoch ist damit keinesfalls die optimale Einkaufsmenge exakt ermittelbar, dies geht nur bei einfachen stochastischen Nachfragefunktionen (für eine Lösung mit Hilfe von Monte-Carlo-Simulationen siehe beispielsweise Microsoft 2003) ebenso wie die Analyse und Optimierung von Investitionsvorhaben in Hinblick auf die Erfolgswahrscheinlichkeit oder Finanzierung der Investition [vgl. beispielsweise Duscher/Meyer/Spitzner 2012 sowie Romeike/Hager 2009 sowie Romeike/Hager 2013].
Weiterführende Literaturhinweise:
- Duscher, I./Meyer, M./Spitzner, J. (2012): Volatilität kalkulieren und steuern im Sinne eines wertorientierten Investitionscontrollings, in: Zeitschrift für Controlling und Management, Sonderheft 2, Juli 2012, S. 46-51.
- Grinstead, C. M./Snell, J. L. (1997): Introduction to Probability, American Mathematical Society, 1997.
- Hubbard, D. (2007): How to Measure Anything: Finding the Value of Intangibles in Business, Hoboken 2007.
- Kaiser, H./Nöbauer, W. (1998): Geschichte der Mathematik, Wien 1998.
- Metropolis, N. C./Ulam, S. (1949): The Monte Carlo Method, Journal of the American Statistical Association, Vol. 44, No. 247, (Sep. 1949), S. 335-341.
- Microsoft (2003): Introduction to Monte Carlo simulation, http://office.microsoft.com/en-us/excel/HA011118931033.aspx
- Romeike, F. (2010): Risikoadjustierte Unternehmensplanung – Optimierung risikobehafteter Entscheidungen basierend auf stochastischen Szenariomethoden, in: Risk, Compliance & Audit, 06/2010, S. 13-19.
- Romeike, F./Spitzner, J. (2013): Von Szenarioanalyse bis Wargaming, Betriebswirtschaftliche Simulationen im Praxiseinsatz, Weinheim 2013.
- Romeike, F./Hager, P. (2009): Erfolgsfaktor Risk Management 2.0 – Methoden, Beispiele, Checklisten: Praxishandbuch für Industrie und Handel, 2. Auflage, Wiesbaden 2009.
- Romeike, F./Hager, P. (2013): Erfolgsfaktor Risk Management 3.0 – Methoden, Beispiele, Checklisten: Praxishandbuch für Industrie und Handel, 3. Auflage, Wiesbaden 2013.
- Ulam, S./Richtmyer, R. D./von Neumann, J. (1947): Statistical methods in neutron diffusion, in: Los Alamos Scientific Laboratory report LAMS-551; Los Alamos 1947.
